量子複合系におけるファノ効果

1. はじめに

メゾスコピック系とは，大きさが数10μｍ程度から数nm程度の系に現れる量子力学的効果を研究する分野のことです。この分野の最大の特長は，系を自在にデザインし，制御性の高い実験を行うことにより，量子力学の本質に迫るような研究が出来る点にあります。

たとえば，物質が波動性と粒子性をあわせ持つ，という二重性は，量子力学において本質的なものです。
しかし，実際に，両方の性質が同時に顔を出すような状況に出会うことは稀です。
例えば，光の干渉効果を説明するためにはその波動性を考えれば良いし，光電効果を説明するためにはその粒子性に着目すれば良い，という具合です。

それでは，両方の性質が同時に現れざるを得ないような状況では，どのような現象が起こるのでしょうか？

ここでは，その一例として，典型的なメゾスコピック系であるアハラノフ・ボームリング（Aharonov-Bohm Ring, AB ring）と量子ドット（Quantum Dot, QD）を組み合わせた系を舞台として行った，電子の二重性についての実験を紹介しましょう。

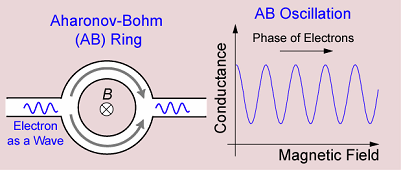
ABリングとは...

非常に小さいリング状の導体の電気伝導度は，リングを貫く磁場によって周期的に振動（AB振動）します。
これは電子波の位相が磁場によって変調されるためで，電子の波動性が劇的に現れる例の一つです。
光の波動性を明らかにした実験にヤングの二重スリットの実験がありますが，ABリングはその電子版であるといえます。

典型的なABリングの直径は１μｍ，幅は0.1μｍ，AB振動が観測される温度は100mK程度です。

量子ドットとは...

電子を非常に小さい領域（ドット）に閉じ込めたとしましょう。
すると，条件さえととのえば，その傍にあるゲート電圧を制御することで，ドットに含まれる電子数を1個ずつ変化させることが出来ます。このとき，そのドットのことを量子ドットと呼びます。
量子ドットの電気伝導度は下右図のようなクーロン振動（Coulomb Oscillation）という周期的な変化を示します。

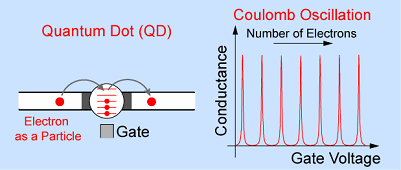
このような現象の背後では，「単電子効果」と「閉じ込め効果」の二つが重要な役割を果たしています。
そして，その結果，「原子に導線をつなぎ，特定の軌道のみを通過する伝導現象を観測する」ことと同様の現象が起きているのです。
このことから，量子ドットのことを「人工原子（Artificial Atom）」と呼ぶこともあります。
その意味で量子ドットとは，まさに電子の粒子性があらわになっている系であるといえるでしょう。

半導体量子ドットの典型的な大きさは100nｍ程度であり，クーロン振動が観測されるのは1K以下です。

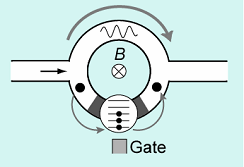
2. 量子ドット-ABリング複合系

量子ドットとABリングは，それぞれ電子の粒子性と波動性を代表する典型的なメゾスコピック系です。
それでは，その２つを組み合わせた複合系はどのような性質を示すのでしょうか。

このような複合系（下図）については，1990年代半ばから盛んに研究が行われてきました。しかし，それらの研究の主題は，「量子ドットを通過する際に電子波の位相がどのように変化するか」というものであり，ABリングは脇役にすぎませんでした。

しかし，ここで若干の疑問が起きます。
というのも，今，ABリングと量子ドットとは量子力学的に不可分に組み合わされているわけだから，「本当は，ABリングは系の性質に本質的な寄与を生じるのではないか」という疑問です。

実は，このような複合系では「ファノ効果（Fano Effect）」が起きると予想されるのです。
ファノ効果とは，系に離散状態と連続状態があるとき，遷移確率Tが特徴的な非対称な形状となるもので，共鳴と干渉が同時に起こる量子力学的な現象です。
非対称な形状をあらわす式を下に示しました。これはファノの式と呼ばれています。また，式中のqはファノの非対称性パラメータと呼ばれています。

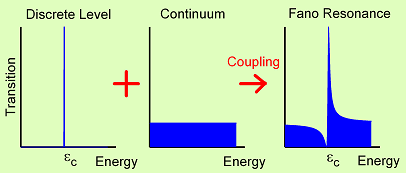
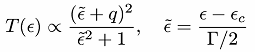
量子ドット-ABリング複合系の場合，離散状態は量子ドットから生じ，連続状態はABリングを構成する電子系に相当します。
下左図に示すように，複合系の左側にいた電子が右側に「遷移」する際，量子ドットを通る経路と通らない経路（ここでは簡単に「アーム（Arm）」と呼びましょう）の二つがあり，その二つの過程が干渉することでファノ効果が起きるだろう，というわけです。

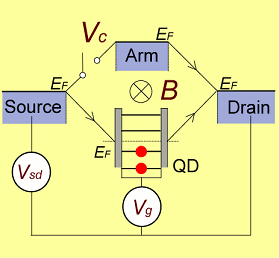
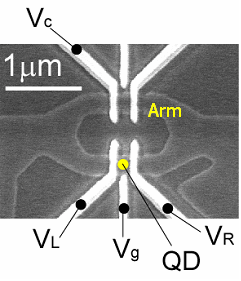
右上図は，メゾスコピック系におけるファノ効果を検証するために作製したサンプルの走査型電子顕微鏡写真です。
ABリングはAlGaAs/GaAs二次元電子系を削り取って（化学エッチング）形成されており，下側の経路に量子ドット（●）を持っています。 ドット内の電子数は大体80〜100個程度です。

3. メゾスコピック・ファノ効果

図に典型的な結果を示しました。これは系の伝導度を，ドットの傍のゲート電極電圧の関数としてプロットしたものです。複合系は30mKという極低温にあります。

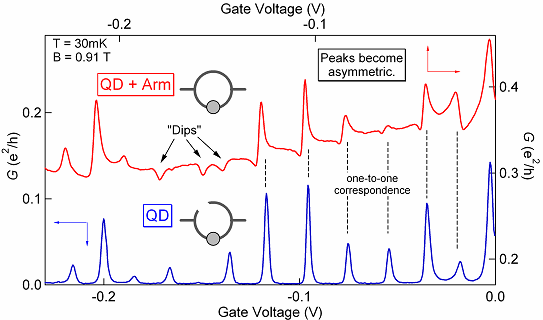
この図の下のデータ（青）は，別の電極によってABリングの量子ドットが無い方の経路（アーム）を遮断し，電子が量子ドットのみを通過するようにした場合の伝導度を示しています。
スパイク状の伝導度は，典型的なクーロン振動を表しています。

次に，アームも電子が通れるようにしてみましょう。
そのときの伝導度が，図の上のデータ（赤）です。
上と下のデータは，ピーク位置に関しては良い一対一対応を示しているにも関わらず，上のデータでは，ピーク形状が一方に裾を引いた極めて非対称な形になっています。
また，あるゲート電圧では，ピークではなく単なるくぼみになっていることもわかります。

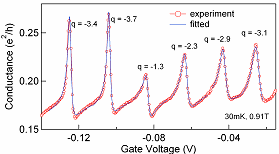
これらのピーク形状をファノの式でフィットしたものを上に示しました。赤がデータで，青がフィットした結果です。
この一致は満足すべきもので，この系で確かにファノ効果が起きており，量子ドット中の離散状態とABリングの連続状態を同時に電子が通過し，干渉を起こしていることがわかります。
言い換えれば，量子ドットの離散状態とABリングの連続状態とが重ね合わされた量子状態（ファノ状態）が実現していることを意味しています。

ここまでで，この複合系がメゾスコピックサイズのファノ系であることを示しました。
実は，ファノ効果自体は，極めて普遍的に観測される現象です。
たとえば，ラマン散乱，光電子放出，原子の光電離，励起子吸収，中性子散乱などで観察されています。
しかし，この複合系はファノ効果を示す単一サイトの系としては，これまでで最大のものです。また，電気伝導現象でこれほど明瞭なファノ効果が観測されたのも初めてです。

4. デコヒーレンスによるファノ状態の消失

メゾスコピック系の特長はその制御性にあります。
制御することによって，ファノ効果のどのような性質が現れるのでしょうか？

ここでは，ファノ効果をあえて「壊してみる」ことによって，ファノ状態にコヒーレンスが必要であることを検証してみましょう。

コヒーレンス（Coherence）とは，「電子が干渉性を保っていること」を意味しています。言い換えれば，電子が波としての性質を失わないでいることです。逆にデコヒーレンスとは，「電子が干渉性を失うこと」を意味しています。

有限温度におけるファノ効果

系にデコヒーレンスを導入する方法の一つとして，系の温度を上昇させる方法があります。
下の図に，温度を50mKから450mKに上昇させたときの複合系の伝導度を示しました。

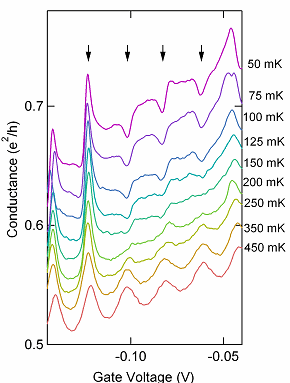
50mKでは，図に矢印で示したように，伝導度は特徴的なファノの形状を示します。
しかし，温度の上昇とともに，ファノの形状は無くなり，左右対称なピークになってきます。
これは，温度上昇によって系からコヒーレンスが失われると，ファノ状態が消失することを意味しています。
高温では単に量子ドットとアームの古典的な並列回路になってしまうのです。

非平衡ファノ効果

デコヒーレンスを導入する他の方法としては，系に電位差（バイアス）をかけ，系を非平衡状態に置く方法があります。

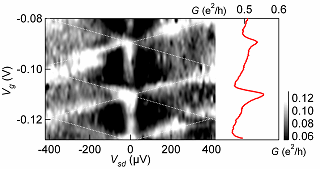
上の図はゲート電圧とバイアスの関数として，複合系の微分伝導度をグレイスケールプロットで表示したもので，白い部分が高い伝導度を表しています。
点線で示したようなひし形の構造（量子ドットに特有のもので「クーロンダイアモンド」と呼ばれます）が現れます。
それとともに，ゼロバイアス付近に伝導度の高い部分が現れています。
図の右側にゼロバイアスにおける非対称クーロン振動を示しましたが，ファノ効果による非対称な裾に対応して，伝導度の高い部分が生じていることが分かります。
このことは，この低バイアス領域では，量子ドットが電子数固定の状態にあっても，コヒーレントなファノ状態を介して電子がドットを通過出来ることを意味しています。
そして，高バイアスにおいては伝導が生じないこともわかります。
これは有限のバイアスによって複合系全体のコヒーレンスが保たれなくなり，ファノ状態がもはや存在しなくなったことを表しているのです。

このように，「系にデコヒーレンスを導入する」ことによってファノ効果が消失することを見ました。
このような制御が出来るのは，メゾスコピック系ならでは，といえるでしょう。

5. ファノ効果の位相制御

実は，メゾスコピックならではの利点はもう一つあります。
ファノ効果そのものは普遍的な現象である，と述べました。
しかし，他の様々なファノ効果を起こす系と比べて，私たちのファノ系が最も異なっているのは，離散準位と連続状態が空間的に分離している点にあります。
このことは，両者の位相差を制御できることを意味しています。
位相制御は，たとえば，磁場によって行うことができます（AB効果）。
図にその結果を示します。高さは伝導度，一方の横軸は磁場，他方はゲート電圧です。

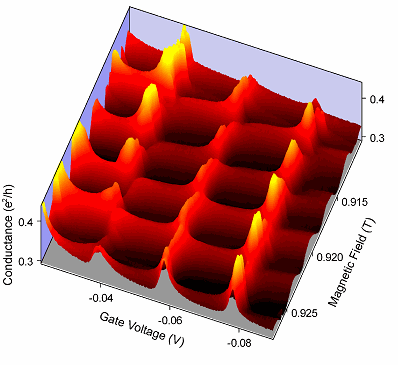
この図は，ゲート電圧を固定して磁場を変化させるとAB振動が現れ，逆に磁場を固定してゲート電圧を変化させるとクーロン振動が現れることを示しています。
磁場は電子波の位相，つまり電子の波動性を制御し，ゲート電圧は量子ドット内の電子数，つまり電子の粒子性を制御するものです。
この意味で，この図はファノ効果を仲立ちとして電子の二重性（duality）がはっきりと浮かび上がったものである，と言ってよいでしょう。

さらに下の図に，特定の磁場でのファノの形状を示しました。

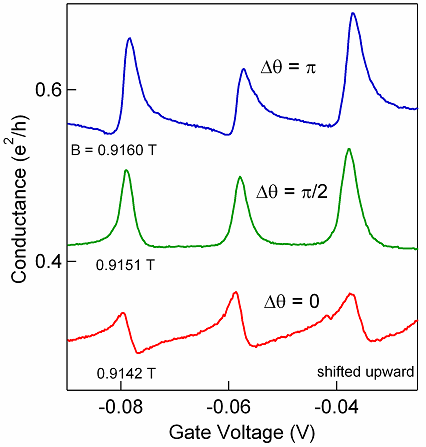
この図から，磁場を少し変化させると，非対称性の向きが逆になることがわかります。
また，その途中で全く対称なピーク形状になることもわかります。
詳細は省きますが，この現象を統一的に理解しようとすれば，ファノの非対称性のパラメータとして知られる量qを，実数ではなく，複素数に拡張しなければならないことがわかります。
このことはファノの理論と矛盾するものではないのですが，分光学においてqが長らく実数として扱われてきたことを考えると，今回，実験的に初めて検証された新しい知見であると言えるでしょう。