
AB効果は,電子の波動性の表れであり,それ自体大変興味深い現象ですが, AB効果とそれ以外の効果を組み合わせれば,さらに面白いことが起きるのではないかと期待できます. 例えば,このAB効果と量子ドットにおける単電子効果を組み合わせることで,ファノ効果を観測することができます. これについては,量子ドット-ABリング複合系におけるファノ効果をご参照ください.
ここではAB効果と,スピン軌道相互作用を組み合わせることを考えてみましょう. スピン軌道相互作用とは何でしょうか. 特殊相対性理論からは,「動いている荷電粒子には電場が磁場に見える」ことが導かれます. その結果生じる「有効磁場」を通じて,粒子の運動が粒子の内部自由度であるスピン状態に影響を及ぼします. これがスピン軌道相互作用です. 有効磁場の大きさや向きは,物質の種類や構造によって変化します. 近年では,スピンを利用したエレクトロニクス,いわゆるスピントロニクスの研究分野において スピン軌道相互作用の利用が積極的に考えられ,実験的にも外部磁場なしでのスピン歳差運動の実現やスピンホール効果の観測などに繋がっています.
われわれは実験の舞台として,強いスピン軌道相互作用を示すことが知られている二次元正孔系を用いました.
分子線エピタキシーによって結晶成長した二次元正孔ヘテロ構造基板上に,
リソグラフィーとエッチング技術を用いて写真にあるようなアンチドット格子を作製しました.
アンチドット格子とは,規則的に基板を円形(写真では直径250 nm)の窪みがあいた構造です.
窪みになった部分には強いポテンシャル障壁が形成され(右図),キャリアは存在することができません.

磁場中でのアンチドット格子の電気伝導を調べると,単一リングの場合とよく似た周期的振動を示すことが知られています. これをAB振動と呼びたくなるところですが,実は,単純にリングを沢山並べた構造ではAB振動は消失することが知られており, アンチドット格子でなぜこのような振動が観測されるのかは,ちょっとした謎です. そこで,アンチドット格子の電気伝導における振動を,通常のAB振動と区別するために,AB型振動と 呼ぶことにします. ここでは,その起源の詳細には立ち入らないことにしますが,アンチドット格子を用いることで,単一リングの測定につきまとう, 「サンプルに依存する効果(測定試料ごとに散乱体の配置が異なったり,リング形状が厳密に一定でないことに起因する効果)と, 依存しない本質的な効果の識別」という問題を軽減できると考えられます. アンチドット格子では,多数リングを同時測定しているようなものなので,サンプル依存の効果は打ち消されてしまうからです.
低温での測定結果を見てみましょう.
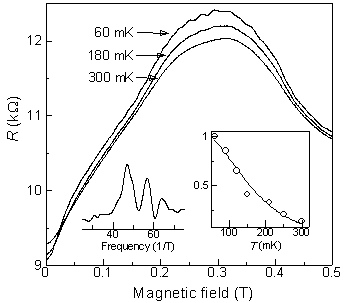
温度が下がるにつれ,磁気抵抗に振動成分が現れていることが分かります.これがAB型振動です.
0.3 T付近に存在する幅広のピーク構造は整合性ピークと呼ばれるもので,ここでは取り扱いません.
振動成分を抜き出して,フーリエ変換を施すと,50 T -1付近に複数のピークを持つことが分かります.
アンチドット一個の直径を考慮すると,AB型振動であってもこの付近にピークを持ちますが,その数は一本のはずです.
従ってこの実験結果は,AB型振動が,AB効果以外の効果によって変調を受けたと考えることができます.
このAB効果以外の効果が,スピン軌道相互作用によるものであることを,
簡単なモデルによって検証してみることにします.
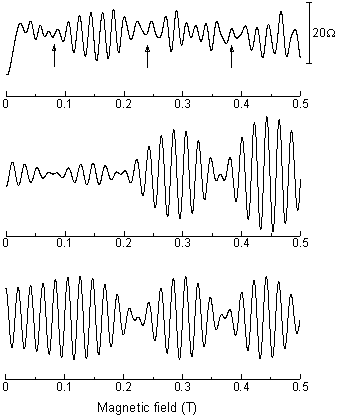
下図の一番上は,測定された磁気抵抗から80 T -1以下の振動成分を抜き出したものです.
振動が矢印で示されたような「節」を持ち,変調されていることが分かります.
スピン軌道相互作用を考慮すると,AB型振動の変調は次式のように書くことができます.
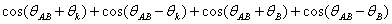
ここでθABは通常のAB型振動による位相です.
θkは,スピン軌道相互作用から予想される付加的な位相のうち,バンド分裂に起因します.
一方,θBは,スピンが閉経路を周回する際に獲得する幾何学的位相で,ベリー位相とも呼ばれます.
実験から得られた値を用いてこの式をプロットすると,真ん中の図になります.
節の位置をよく再現することが分かります.
高磁場側で振幅の違いが大きくなることは,この式が厳密には低磁場域のみで適用可能なためです.
図の一番下は,式からベリー位相の項を省いた場合の結果で,実験とは一致しません.
この結果,スピン軌道相互作用,特にベリー位相を取り入れることで,実験結果を理解できることが分かりました.
ベリー位相の効果を,固体物理の実験から観測することは非常に珍しく, その意味でも大変興味深い結果ということができるでしょう.